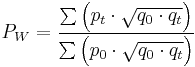List of price index formulas
A number of different formulas, more than hundred, have been proposed as means of calculating price indexes. While price index formulas all use price and possibly quantity data, they aggregate these in different ways. A price index aggregates various combinations of base period prices (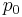 ), later period prices (
), later period prices (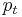 ), base period quantities (
), base period quantities (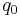 ), and later period quantities (
), and later period quantities ( ). Price index numbers are usually defined either in terms of (actual or hypothetical) expenditures (expenditure = price * quantity) or as different weighted averages of price relatives (
). Price index numbers are usually defined either in terms of (actual or hypothetical) expenditures (expenditure = price * quantity) or as different weighted averages of price relatives (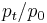 ). These tell the relative change of the price in question. Two of the most commonly used price index formulas were defined by German economists and statisticians Étienne Laspeyres and Hermann Paasche, both around 1875 when investigating price changes in Germany.
). These tell the relative change of the price in question. Two of the most commonly used price index formulas were defined by German economists and statisticians Étienne Laspeyres and Hermann Paasche, both around 1875 when investigating price changes in Germany.
Contents |
Laspeyres
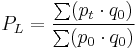 .
.
This compares the price of the old basket of goods  for the old and new prices.
for the old and new prices.
Paasche
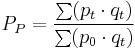 .
.
This compares the price of the new basket of goods  for the old and new prices.
for the old and new prices.
Unweighted indexes
Unweighted price indexes or elementary price indexes only compare prices between two periods. They do not make any use of quantities or expenditure weights. These indexes are called "elementary" because they are often used at the lower levels of aggregation for more comprehensive price indexes.[1] At these lower levels, weights are not necessary since only one type of good is being aggregated.
Carli
Developed in 1764 by Carli, an Italian economist, this formula is the arithmetic average of the price relative between a period t and a base period 0.
Dutot
In 1738 French economist Dutot proposed using an index calculated by dividing the average price in period t by the average price in period 0.
Jevons
In 1863, English economist Jevons proposed taking the geometric average of the price relative of period t and base period 0.[2] When used as an elementary aggregate, the Jevons index is considered a constant elasticity of substitution index since it allows for product substitution between time periods.[3]
Harmonic mean of price relatives
The harmonic average counterpart to the Carli index.[4] The index was proposed by Jevons in 1865 and by Coggeshall in 1887.[5]
Carruthers, Sellwood, Ward, Dalén index
Is the geometric mean of the Carli and the harmonic price indexes.[6] In 1922 Fisher wrote that this and the Jevons were the two best unweighted indexes based on Fisher's test approach to index number theory.[7]
Ratio of harmonic means
The ratio of harmonic means or "Harmonic means" price index is the harmonic average counterpart to the Dutot index.[4]
Precision Formulas
Marshall-Edgeworth
The Marshall-Edgeworth index, credited to Marshall (1887) and Edgeworth(1925),[8] is a weighted relative of current period to base period sets of prices. This index uses the arithmetic average of the current and based period quantities for weighting. It is considered a pseudo-superlative formula and is symmetric.[9] The use of the Marshall-Edgeworth index can be problematic in cases such as a comparison of the price level of a large country to a small one. In such instances, the set of quantities of the large country will overwhelm those of the small one.[10]
Superlative indices
Superlative indices treat prices and quantities equally across periods. They are symmetrical and provide close approximations of cost of living indices and other theoretical indices used to provide guidelines for constructing price indices. All superlative indices produce similar results and are generally the favored formulas for calculating price indices.[11] A superlative index is defined technically as "an index that is exact for a flexible functional form that can provide a second-order approximation to other twice-differentiable functions around the same point."[12]
Fisher
This is also called Fisher's “ideal” price index.
Törnqvist
The Törnqvist or Törnqvist-Theil index is the geometric average of the n price relatives of the current to base period prices (for n goods) weighted by the arithmetic average of the value shares for the two periods.[13][14]
Walsh
The Walsh price index is the weighted sum of the current period prices divided by the weighted sum of the base period prices with the geometric average of both period quantities serving as the weighting mechanism:
Notes
- ^ PPI manual, 598.
- ^ PPI manual, 602.
- ^ PPI manual, 596.
- ^ a b PPI manual, 600.
- ^ Export and Import manual, Chapter 20 p. 8
- ^ PPI manual, 597.
- ^ Export and Import manual, Chapter 20, p. 8
- ^ PPI manual, Chapter 15, p. 378.
- ^ PPI manual, 620.
- ^ PPI manual, Chapter 15, p. 378
- ^ ILO CPI manual, Chapter 1, p. 2.
- ^ Export and Import manual, Chapter 18, p. 23.
- ^ PPI manual, p. 610
- ^ “Tornqvist Index and other Log-change Index Numbers”, Statistics New Zealand Glossary of Common Terms.
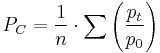
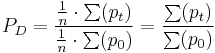
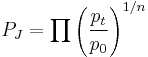
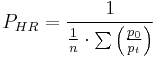
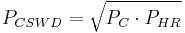
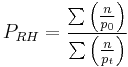
![P_{ME}=\frac{\sum [p_{c,t_n}\cdot \frac{1}{2}\cdot(q_{c,t_0}%2Bq_{c,t_n})]}{\sum [p_{c,t_0}\cdot \frac{1}{2}\cdot(q_{c,t_0}%2Bq_{c,t_n})]}=\frac{\sum [p_{c,t_n}\cdot (q_{c,t_0}%2Bq_{c,t_n})]}{\sum [p_{c,t_0}\cdot (q_{c,t_0}%2Bq_{c,t_n})]}](/2012-wikipedia_en_all_nopic_01_2012/I/e515d0e7538c85a2befe28ec587a2de1.png)
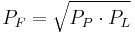
![P_t = \prod_{i=1}^{n}\left(\frac{p_{it}}{p_{i0}}\right)^{\frac{1}{2} \left[\frac{p_{i0}q_{i0}}{\sum_{i=1}^{m}\left(p_{i0}q_{i0}\right)}%2B \frac{p_{it}q_{it}}{\sum_{i=1}^{m}\left(p_{it}q_{it}\right)}\right]}](/2012-wikipedia_en_all_nopic_01_2012/I/a62287087b16de6c13ab473cfdd55b4a.png)